what must you vary in order to obtain a beers law plot


Instrumental Deviation from Beer's Law
Excel and OpenOffice Calc Versions
| Screen animation of version 1. Click to enlarge. |  Screen animation of version 2. Click to enlarge. |  Screen animation of version 3. Click to enlarge. |
[Assumptions] [Background] [Frequently Asked Questions] [Student handout] [WingZ version]
This spreadsheet is a numerical simulation of absorption spectroscopy. It computes the measured absorbance and plots the analytical curve (absorbance vs concentration) for a simulated cushion measured in an absorption spectrophotometer with variable wavelength, spectral bandpass and unabsorbed devious light, given the maximum absorptivity, path length, and half-width of the absorber, and the slit width and per centum unabsorbed devious low-cal of the monochromator. The arrow buttons beneath each of these parameters permit you to modify the values quickly without typing. The spectra and the belittling bend change dynamically equally the variables are changed. Any list of concentrations can be typed in for the belittling bend. The spreadsheet fits a direct line to the calibration curve and calculates the slope, intercept, the correlation coefficient R 2 , and the percent relative error in predicting concentrations from the fitted line.
Alternative versions: Version 1 is the basic (simplest) version. The optional Version ii allows the user to select which quantity to plot vs concentration:absorbance (log(Io/I)), transmission (I/Io), absorbed intensity (Io-I), or I and Io separately. This version can be used to demonstrate the utility of computing absorbance. Version 3 includes optional random noise in the measurement of light intensity (photon and/or detector noise), which is more realistic.
Assumptions of this simulation: The truthful monochromatic absorbance is assumed to follow the Beer-Lambert Law; the cushion spectrum consists of two peaks, at fixed wavelengths of 150 and 300 nm, that accept either Gaussian or Lorentzian shape (selectable past user); the spectral width of the light source is much greater than the monochromator spectral bandpass; the monochromator has a triangular slit function (i.e. the entrance and go out slits are equal in width and are rectangular in shape); the assimilation path length and cushion concentration are both compatible across the calorie-free beam; the spectral response of the detector is much wider that the spectral bandpass of the monochromator. Only version 3 includes the issue of random noise (encounter Signal-to-noise ratio of absorption spectrophotometry, Issue of Slit Width on Signal-to-Dissonance Ratio in Absorption Spectroscopy, and Comparison of Scale Curve Fitting Methods in Absorption Spectroscopy for other simulations that include random dissonance).
Annotation: In the quantitative analysis of known absorbers, these instrumental deviations from Beer's Law can be avoided computationally by applying curve-plumbing fixtures to the spectra, rather than to the scale curve, using the Manual Plumbing fixtures (TFit) Method.
View Equations (.pdf)
Download Version 1: in OpenOffice format (.ods) ; in Excel format (.xls)
Download Version 2: in OpenOffice format (.ods) ; in Excel format (.xls)
Download Version 3: in OpenOffice format (.ods); in Excel format (.xls)
WingZ Versions
Other related simulations:
Comparison of Scale Bend Fitting Methods in Absorption Spectroscopy
Bespeak-to-noise ratio of absorption spectrophotometry
Event of Slit Width on Point-to-Noise Ratio in Assimilation Spectroscopy
Fault propagation in Analytical Scale
Spectroscopic Simulation of Diminutive Absorption
Worksheets for linear and non-linear calibration curves for your own data
TheTransmission Fitting (TFit) Method applies curve fitting to the spectra rather than the calibration data.
[Render to Index]
Background
The Beer-Lambert Constabulary. In absorption spectroscopy, the intensity I of lite passing through an absorbing sample is given by the Beer-Lambert Law:
I = Io*x-(alpha*L*c)
where �Io� is the intensity of the light incident on the sample, �alpha� is the absorption coefficient or the absorptivity of the absorber, �Fifty� is the distance that the light travels through the fabric (the path length), and �c� is the concentration of absorber in the sample. The variables I, Io, and alpha are all functions of wavelength; L and c are scalar. In conventional applications, measured values of I and Io are used to compute the absorbance, divers as
A = log(Io/I) = alpha*L*c
Absorbance defined in this way is (ideally) proportional to concentration, which simplifies analytical calibration.
The absorption coefficient alpha is adamant experimentally. If you solve the above equation for alpha, you get:
alpha = A/(L*c)
And then by measuring the absorbance A of a known concentration c of the absorbing chemical compound using an absorption path length 50, you can summate alpha. Because A has no units (it's the log of a ratio of two intensities, so the intensity units abolish out), the units of blastoff are the reciprocal of the units of Fifty and c. For example, if the path length L is in cm and the concentration c is in moles/liter, alpha is in liters/mole-cm. Even amend is to gear up a series of solutions at different concentrations and plot the measured absorbances vs the concentrations; the resulting plot is called a calibration curve or belittling bend. The slope of this bend is blastoff*L, and so if you measure the slope and divide by 50, you have alpha.
Deviations from the Beer-Lambert Law. It's important to understand that the "deviations" from the Beer-Lambert Constabulary discussed hither are non actually failures of this law simply rather credible deviations caused by failures of the measuring musical instrument to attach to the status nether which the law is derived. The fundamental requirement under which then Beer-Lambert Police is derived is that every photon of light striking the detector must have an equal chance of absorption. Thus, every photon must have the same absorption coefficient alpha, must laissez passer through the aforementioned absorption path length, L, and must experience the aforementioned cushion concentration, c. Anything that upsets these atmospheric condition volition lead to an credible deviation from the constabulary.For example, whatever real spectrometer has a finite spectral resolution, meaning that an intensity reading at one wavelength setting is actually an average over a pocket-sized spectral interval called the spectral bandpass. Specifically, what is actually measured is a convolution of the true spectrum of the absorber and the instrument function. If the absorption coefficient alpha varies over that interval, and then the calculated absorbance volition no longer exist linearly proportional to concentration (this is called the polychromatic radiation result). This effect leads to a general concave-down curvature of the analytical curve.
Another source of instrumental non-ideality is stray light, which is whatever light striking the detector whose wavelength is outside the spectral bandpass of the monochromator or which has not passed through the sample. Since in most cases the wavelength setting of the monochromator is the pinnacle absorption wavelength of the analyte, information technology follows that any lite outside this range is less captivated. The nearly serious issue is caused by stray light that is not absorbed at all by the analyte at all; this is called unabsorbed devious light. This effect also leads to a concave-downwards curvature of the belittling bend, but the effect is relatively minor at depression absorbances and increases quickly at high absorbances. Ultimately, unabsorbed stray calorie-free results in a apartment plateau in the analytical bend at an absorbance of -log(fsl), where fsl is the partial stray light.
In that location are other potential sources of deviation that are not included in this simulation, either because they are normally not so serious under the weather of typical laboratory applications of absorption spectrophotometry, or because they can be avoided by proper experiment design. These are:
(a) unequal light path lengths across the calorie-free beam. (In near laboratory applications, the samples are measured in foursquare cuvettes (sample vessels) to insure a constant path length for all photons. When round test-tube sample cells are used, the light beam passing through the sample is restricted to a the key region of the sample tube in order to minimize this effect);
(b) unequal absorber concentration across the low-cal beam. (Solution samples are carefully mixed before measurement to insure homogeneity);
(c) changes in refractive alphabetize at high analyte concentration (most analytical applications operate at lower concentrations);
(d) shifts in chemical equilibria every bit a office of concentration (solutions may need to be buffered to forestall this, or the measurement can be fabricated at the "isosbestic indicate", or a multicomponent analysis may be performed if the spectra of all the species in equilibrium tin be determined);
(east) fluorescence of the sample, in which some of the absorbed light is re-emitted and strikes the detector (most analytes are non fluorescent, but if and then, this error can be reduced by using a spectrophotometer that places the sample betwixt the calorie-free source and the monochromator, such equally a photodiode-array spectrometer);
(f) light-scattering by the sample matrix, especially in turbid samples (this is a mutual source of variable background assimilation, which tin be reduced by using a spectrophotometer that places the sample cuvette right upwardly against the face of the detector so that it captures and detects a large fraction of the scattered light).
(g) if the low-cal intensity is extremely high (like a focused laser), it's possible to detect not-linear optical effects, which are a primal failure of the Beer-Lambert Law. This will happen, for example, as the absorber approaches optical saturation (equal populations of molecules in the ground and excited states), in which case the sample no longer absorbs low-cal.
The simulation hither includes only the two most common instrumental deviations from Beer'southward Police force: polychromaticity and unabsorbed stray calorie-free errors. The simulation operates like any numerical integration, by slicing up the spectral range viewed by the detector into a big number of modest slices and bold that the Beer-Lambert Police applies over each small piece separately. The sample absorption is represented in this simulation past a unmarried absorption band of either Gaussian or Lorentzian shape (selectable by the user) and adjustable width. The spectral bandpass of the monochromator is represented past a triangular function of adaptable width. And then all the split up slices are summed up to represent the incident and transmitted light indicate measured past the detector. Every bit it turns out, i does not demand to use very many slices to obtain a expert model of the operation of a typical assimilation spectrophotometric measurement (5 nm slices are used in this instance).
The calibration curve. In principle, it is possible to decide the concentration of an unknown solution of by solving the in a higher place equation for concentration:
And then, you lot could calculate the concentration c by measuring the absorbance A and dividing itpast the product of the path length L and absorptivity blastoff. That is, if you know blastoff. Values of blastoff are tabulated for many common molecules, but the trouble is that alpha varies as a function of wavelength, temperature, solvent, pH, and other chemic atmospheric condition, so if the conditions of your sample don't match those with which the alpha was measured, the calculated concentration won't be correct. Also, the absorbances measured on your instrument may non vary linearly with concentration, due to the deviations discussed in a higher place, in which example no single value of blastoff would give authentic results. Every bit a result, information technology is much more than mutual in exercise to prepare a series of standard solutions of known concentration, whose chemical weather condition equally close as possible to those of the sample, mensurate their absorbances on your instrument, and plot a calibration curve with concentration of the standards on the x-axis vs measured absorbance on the y-axis. (If Beer's Constabulary is observed, the slope of this bend is
alpha*L).In one case the scale curve is established, unknown solutions can be measured and their absorbances converted into concentration using the calibration curve. Here is a graphic animation of this calibration process. This can be washed either graphically (by cartoon a line from the absorbance of each unknown across to the scale curve and and then downward to the concentration axis) or it tin be washed mathematically (by plumbing fixtures a line or curve to the calibration data, solving the equation of that line for concentration, then using that equation to catechumen measured absorbances to concentration). With computers, it's ordinarily easier to exercise the latter. (See "Comparison of Calibration Curve Plumbing fixtures Methods in Assimilation Spectroscopy" to see how to fit non-linear calibration curves). The important bespeak is that fifty-fifty if Beer'south Law is not obeyed, y'all tin become accurate resulting using a calibration curve.
Student handout for OpenOffice version.
Instrumental Deviation from Beer's Police force
1. Open http://terpconnect.umd.edu/~toh/SimpleModels/BeersLaw.ods in OpenOffice Calc (August 6, 2008 version or later on). This spreadsheet simulates an optical assimilation spectroscopy measurement and demonstrates how the instrument's measurements of absorbance can deviate from the ideal predicted by the Beer-Lambert Law (a.yard.a. Beer's Law).

The graph on the left of the window shows the absorption spectrum of the analyte in red over a wavelength range from 200 - 400 nm. The blue line is the "Transmitted intensity" ; it shows the spectrum of light emerging from the go out slit of the monochromator and passing through the absorbing sample. Despite its name, a monochromator never really passes a single colour or wavelength of light; it actually passes a pocket-size range of wavelengths. This range of wavelengths is called the "spectral bandpass". The smaller the slit width, the smaller the spectral bandpass, and the more than almost monochromatic is the light emerging from the exit slit. In normal laboratory instruments, the spectral bandpass is controlled past the slit width, which is adjustable by the experimenter on many instruments (but not on the Spectronic twenty, which has a fixed 20 nm spectral bandpass). In this simulation you can vary the slit width of the faux instrument from 10 nm to 100 nm past using the Slit width command above the graph, only it can not be fix below 10 nm (every instrument has a minimum slit width, and therefore a minimum spectral bandpass setting; you can not set the slit width to zero because then no light would go far and the instrument would not work at all! Annotation that the transmitted intensity has a triangular spectral distribution (considering the entrance and exit slit widths are always equal in a normal monochromator.

The peak of the slit office falls at the wavelength setting of the monochromator. Y'all tin control the wavelength setting by using the Wavelength setting control to a higher place the graph; this is equivalent to turning the wavelength knob on the spectrometer.
The other controls above the graph are for the other variables in this simulation, such equally the path length of the absorption cell (i-10 cm). So that you can see how different types of absorbing species would behave, the simulation allows you to vary the maximum absorptivity of the analyte and the spectral width of the cushion (that is, the width of the absorption bands that constitute the absorber's spectrum).
The final command is for the devious light. Every real monochromator passes a small corporeality of white lite as a result of scattering off optical surfaces within the monochromator (mirrors, lenses, windows, and the diffraction grating). Ordinarily this so-called "devious light" is a very small fraction of the light intensity inside the spectral bandpass, only it's of import because it tin can lead to a meaning source of departure from Beer's Police. In most cases the monochromator is tuned to the wavelength of maximum assimilation of the analyte, in order to achieve the greatest sensitivity of analysis. Simply that means that stray light is less absorbed than the low-cal within the spectral bandpass. The worst offender is devious light that is not at all absorbed past the analyte - "unabsorbed stray light", usually expressed as a percentage of the calorie-free intensity within the spectral bandpass. In the simulation, this is ready past the "Unabsorbed devious light" control. Typical monochromators have devious light rating in the 0.01 - 1% range, depending on the wavelength setting and the type of light source used. The stray light is always worse at wavelengths where the calorie-free source is least intense and where the detector is least sensitive. (However, in this simulation, the stray light does not automatically modify with wavelength). Notation: when adjusting the devious light, apply the number spinner (small arrows below the number) rather than typing directly into cell F3. The other variables you can change either by typing or past using the number spinners.

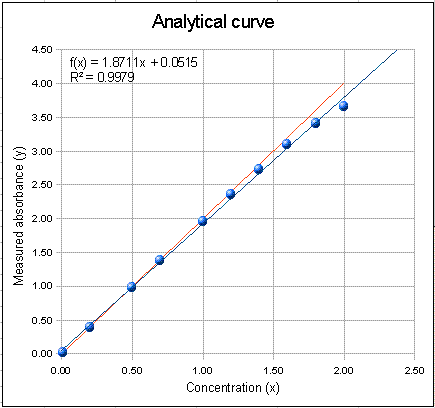
The graph on the right of the window is the analytical curve (calibration curve), showing the absorbances measured for each of the standard solutions listed in the table in the top centre of the window. You can type whatever set up of concentrations in the concentration cavalcade of this table, up to a maximum of 10 standards. The carmine line in the plot (sometimes obscured by the other lines) represents the ideal Beer'southward Police absorbances, the blue dots represent the measured absorbances for each standard solution, and the blue line is the least-squares straight-line fit to the concentration-absorbance data. Ideally, the fitted straight line (blue line) should get correct through the middle of the blue dots. Besides on the plot is the equation of the fitted line (x = concentration and f(ten) = absorbance) and the R two value, which is a mensurate of the degree of correlation betwixt absorbance and concentration (ane.0000 means perfect correlation; anything less than ane.0000 is not perfect).
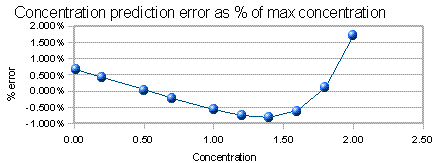
The graph below the scale curve is the concentration prediction error. If you were to run the standards as unknowns and predict their concentrations from the straight-line fit to the calibration curve, this would be the error in prediction, expressed equally a per centum of the highest concentration. (The standard deviation of those errors is a skilful single-number summary of those errors; information technology is displayed to the left). This is a more sensitive indicator of non-linearity than the R two value.
2. Start the experiment with a nearly platonic example (with the spectral bandpass much less than the absorption width and no stray low-cal). Set up wavelength = 300 nm, slit width = ten nm, absorber width = 200 nm, maximum absorptivity = 1, path length = 1 cm, and unabsorbed stray light = 0. Notation that the platonic absorbances (ruby-red line), the measured absorbances (blue dots), and the least-squares fit (bluish line) are essentially identical, even at the highest concentrations, and the R 2 is exactly 1.0000, showing that the musical instrument readings follow Beer's law in this most ideal case. You can see that in this instance the assimilation spectrum is almost apartment over the spectral bandpass. This ways that all the photons accept essentially the aforementioned assimilation coefficient, a primal requirement of Beer'due south Police force. The concentration prediction mistake (the graph below the calibration bend) is and so minor it is negligible compared to other errors that are likely to be greater anyway, such as volumetric calibration accuracy and precision. Simply real-earth absorption measurements are never so perfect.
3. Unabsorbed devious light limit simply. Go out the absorber width = 100 nm, slit width = 10 nm, maximum absorptivity = i, path length = ane cm, and set up the unabsorbed stray calorie-free = 0.1%, using the number spinner - modest arrows below the number - rather than typing directly into cell F3. For comparing, try a devious lite of 1% and 0.01% and find the calibration curve shape. Notice that the measured absorbance bends off from a straight line at the highest concentrations, but however very linear at lower concentrations. Why does the scale curve flatten out at high concentrations? Simple! As the concentrations increases, the intensity of the transmitted light from the spectral bandpass decreases towards zero, simply the unabsorbed devious lite remains at the same intensity considering it is unabsorbed. So eventually at very high concentrations, all that remains in the transmitted light is stray light, which results in an transmittance reading of T = (I+straylight)/(Izero + straylight), which approaches (straylight)/(Izero + straylight) as I approaches zero. See if you can devise a rule that will predict the plateau absorbance for a given stray calorie-free percent.
4. Typical situation in solution spectrophotometry. Fix wavelength = 300 nm, slit width = 20, absorber width = 100, and go out maximum absorptivity = 1, path length = i cm, % devious light = 0.01% Note that analytical curve plot is about perfectly linear (correlation coefficient is ane.0000) upward to a measured absorbance of 2, yet the slope is 2% less than the platonic line (in red). In other words, just because the the analytical bend seems to exist linear does not mean that the measured absorbance equals the ideal height absorbance. (Of course, in most cases you lot don't really need to know the truthful peak absorbance, because nearly all practical applications of absorption spectroscopy in chemical analysis are calibrated by using standard solutions). The concentration prediction error, based on a linear fit, is less than 0.05%. This gives an idea of the mistake that is caused by the slight remainder not-linearly of the calibration bend.
5. Effect of changing the wavelength. Leave everything equally it was, except return the the maximum absorptivity to one.0 and the stray light to 0.01%. Increase the wavelength setting to 350 nm and meet what happens: the scale curve plot has a lower slope, of grade, because the absorptivity is less at 360 nm that at 300 nm. But that's not all. The bend is besides substantially less linear: the R 2 drops to 0.9998 and the concentration prediction error goes upwards most ten-fold to 0.v%. Why should the scale bend be less linear? Call back virtually the total alter in the absorptivity of the analyte over the spectral bandpass (look at how much the cherry line changes nether the blue triangle). When the wavelength is set at a maximum (or a minimum), the total change in absorptivity over the spectral bandpass is less than when the wavelength is set to the side of a ring, where the rate of modify of absorptivity with wavelength is greatest. Then think nigh the requirement that all the photons have essentially the same assimilation coefficient. This effect is called the "polychromatic light" result. You tin can subtract the polychromatic calorie-free by decreasing the spectral bandpass (using a smaller slit width).
Note that the R twois not a very sensitive indicator of non-linearity: even when information technology is only slightly less than 1.000, pregnant non-linearity may exist nowadays. Looking at the concentration prediction error plot (also called the "residue" plot) is more informative that merely looking at the R twovalue.
You might ask why some spectrometers even have adjustable slit widths, when the best linearity and adherence to Beer's Constabulary is observed at the smallest spectral bandpass. Why not just use the smallest slit width setting all the time? The answer is that wider slits let in more than light, which improves the precision of low-cal intensity measurement. See the simulation "Effect of Slit Width on Signal-to-Noise Ratio in Assimilation Spectroscopy" at http://terpconnect.umd.edu/~toh/models/AbsSlitWidth.html for a simulation of this attribute.
six. Measuring higher concentrations at alternative wavelengths. Suppose nosotros wanted to measure some high concentrations, above the usual linear range of the scale curve, without diluting the samples (which would be time-consuming and possibly expensive and error prone) and without using shorter path length cells (which also involves extra cost).
To illustrate this trouble, y'all can simply increment the maximum absorptivity from 1.0 to two.0, which will instantly double all the absorbances. Go out cushion width = 100, source width = 20, % stray calorie-free = 0.01 and increment the maximum absorptivity to 2.0. With the wavelength set to the maximum at 300 nm, the linearity is not so great (R ii= 0.998; concentration prediction error = 0.78%). This is mainly because of devious light, which effects the absorbance above 3.0.
What about irresolute the wavelength of measurement to a less sensitive wavelength. Irresolute the wavelength is quick and doesn't cost anything. But we found in #5 that measuring on the side of a band leads to a great increase in non-linearity. Set the measurement wavelength to 350 nm. This reduces the absorptivity (sensitivity) by about one-half. The linearity in this case is actually improved (R two= 0.9992; concentration prediction error = 0.48%) despite the fact that the polychromatic lite effect is worse at this wavelength, equally you observed in #v. That's considering the stray light consequence is lessened by the reduced absorbance at the higher wavelength. In this instance the stray light upshot is greater than the polychromatic lite effect.
Simply you tin do fifty-fifty better than this. In this particular simulation, the absorber has a minimum in its assimilation spectrum at nigh 225 nm. At that wavelength we take a like sensitivity reduction, which reduces the stray light effect, just the polychromatic light result is much less on the minimum than on the side of the sloping slide of the spectrum. Set the measurement wavelength to 225 nm. You can encounter that the linearity is greatly improved (R 2= 1.000; concentration prediction fault = 0.023%). Then the best approach is to use the superlative wavelength for lower concentrations and the minimum equally the culling wavelength for college concentrations.
7. Atomic absorption. Sometimes information technology is not possible or practical to take the ideal situation where the spectral bandpass is much narrower than the spectral width of the assimilation. For example, in line source atomic absorption spectroscopy, the effective spectral width of the calorie-free source is set past the line width of the hollow cathode lamp (not by the monochromator's spectral bandpass), and the absorber width is determined mainly past the temperature and pressure in the atomizer. As a result, the absorber width is only most 3 times larger than the spectral width of the low-cal source. For example, the line width of the hollow cathode lamp might exist 0.001 nm and the absorber width might be 0.003 nm. To simulate this situation, nosotros'll let 10 units represent 0.001 nm and set the slit width = 10, cushion width = 30 (because it'due south actually simply the ratio of the widths that is important), devious light = 0.1%, and modify the assimilation peak shape to Lorentzian (a meliorate match to the shape of an atomic absorption line in an atomic absorption atomizer).

With these settings, the measured absorbance is half dozen% less than the truthful value, but the linearity is fairly adept (R two= 0.9999) upward to an absorbance of near 2 and the concentration prediction mistake is simply near 0.iii%.
Merely the situation is substantially worse if 1 attempts to practise continuum-source atomic absorption with a medium-resolution spectrometer. In that instance the spectral bandpass might be 10 or more times larger than the assimilation width. Set the absorber width = 10, slit width = 100, and leave the height shape set to Lorentzian. Annotation the linearity is substantially worse: (R 2= 0.97; concentration prediction error = 5.half-dozen%). This is ane reason why continuum-source atomic assimilation utilizes high-dispersion "echelle" spectrometers that can achieve a spectral bandpass about 10 to 100 times smaller than conventional monochromators at the aforementioned slit width. Note: there are other spectroscopic complexities with line-source diminutive absorption: seeSpectroscopic Simulation of Diminutive Absorption for a more specific simulation of atomic absorption.
eight. Extensions and next steps. Several extensions of this line of investigation might be taken:
a. The simulation "Effect of Slit Width on Signal-to-Noise Ratio in Absorption Spectroscopy" considers how the slit width and the dispersion on the monochromator effects the precision and signal-to-noise ratio of intensity and absorbance measurement. b. "Signal-to-noise ratio of absorption spectrophotometry" provides a more detailed model of a UV-visible absorption spectrophotometer with a continuum source (e.g. tungsten incandescent lamp, modeled as a blackbody), dispersive monochromator, and a photomultiplier detector.
c. "Comparison of Calibration Bend Fitting Methods in Absorption Spectroscopy" compares 3 different methods of fitting the scale bend non-linearity in assimilation spectroscopy.
- d. Ii simulations consider the extension to multi-wavelength information such every bit would be acquired on diode-array, Fourier transform, or calculator-automated scanning spectrometers:
- "Multiwavelength Spectrophotometric Analysis by Classical Least Squares" considers methods that piece of work when the measured absorption follows Beer's Police.
- "The TFit Method for quantitative absorption spectroscopy", located at http://terpconnect.umd.edu/~toh/spectrum/TFit.html, describes a computational approach that eliminates the calibration bend non-linearity by basing the measurement of absorbance on a model of the actual spectroscopy of the measurement, rather than assuming that the instrument adheres to the limiting instance of zero spectral bandpass and null devious calorie-free.
Oftentimes Asked Questions (taken from actual search engine queries)
1. Exactly what does it hateful to 'follow Beer's Constabulary '?
Basically information technology means that the measured absorbance is proportional to the concentration of the absorber, that is, a plot of absorbance vs absorber concentration is a straight line. Absorbance is defined as log(I o / I), where "I o " is the intensity of the light incident on the sample and "I" is the intensity of the low-cal transmitted through the sample,
2 . What is the equation for absorbance vs concentration?
A = alpha*L*c
where alpha is the assimilation coefficient (or absorptivity), Fifty is the path length of the light through the cushion, and c is the concentration of the absorber. The absorbance A is defined equally log(I o / I), where Io is the intensity of low-cal beam that strikes the absorber and I is the intensity of lite beam afterward information technology passes through the cushion. This is chosen the Beer-Lambert Law or Lambert-Beer Law or Beer-Lambert- Bouguer Constabulary. (Strictly speaking, Beer's Law refers to the human relationship of absorbance and concentration and Lambert'southward Police refers to the relationship of absorbance and path length, but the two are normally combined into one).3. Why does absorbance increment with concentration ?
Because the college the concentration, the more than absorbing molecules are in the light path to absorb the lite. It's like brewing tea: weak tea has a depression concentration of tea dissolved in the hot h2o and a lite color (does not absorb much light). Strong tea has a high concentration of tea and a darker color (absorbs lots of light).
four. What is a Beer's Law calibration curve? How exercise you brand and interpret a Beer'southward Law plot ? Why are most scale curves of Beer'southward Police force rather than Lambert's Constabulary?
The usual Beer's Law plot is a plot of concentration of cushion on the x (horizontal) axis, vs measured absorbance on the y (vertical) axis. This is useful when you desire to determine the concentration of solutions by measuring their absorbance. The slope of this plot is the product of the path length L times the absorption coefficient blastoff where t he slope is divers every bit the ratio of the y-centrality deviation to the x-axis difference betwixt whatever two points on the line. (This is in contrast to a Lambert's Police force plot of path length on the 10 axis vs measured absorbance on the y centrality. This might be useful if you want to determine the path length of an absorber by measuring its absorbance. The slope of that plot would be the production of the absorptivity blastoff times the absorber concentration c).
5. What are the units of the assimilation coefficient, blastoff ?
It depends on the units of concentration and path length. If concentration is measured in moles/liter (molarity) and path length in cm, so the units of the absorption coefficient (also called the molar absorptivity) are liters/mole-cm. If concentration is measured in grams per liter and path length in cm, then the units of the absorption coefficient are liters/gram-cm. If concentration is measured in grams per mL (cubic centimeters) and path length in cm, then the units of the absorption coefficient are mL/gram-cm.
6. How do you know the value of the assimilation coefficient, alpha ?
Assimilation coefficients are determined experimentally and are tabulated for a big number of compounds in chemical science reference works. If you solve the above equation for alpha, you get:
alpha = A / (L*c)
So past measuring the absorbance A of a known concentration c of the arresting compound using an absorption path length L, you can calculate blastoff. Because A has no units (it's the log of a ratio of two intensities, so the intensity units cancel out), and considering L and c are in the denominator, the units of alpha are the reciprocal of the units of L and c. Absorption coefficients vary widely from substance to substance and besides vary with wavelength. Values of alpha are tabulated in the literature and in reference books for many common molecules.
7. What's the departure betwixt 'absorption' and 'transmission' ?
Absorption refers to how much light is lost when passing through an absorber. Transmission refers to how much low-cal remains afterwards information technology passes through. Absorption is expressed as the absorbance, log(Io / I) or every bit the assimilation, (Io-I) / Io , or the percent absorption, 100(Io-I) / Io . Transmission is expressed every bit the transmittance, I / I o , or as the percent transmission, 100(I / Io ). As the absorber concentration goes up, the absorbance and the absorption both go up, but the transmission goes down. Of these, absorbance is the nearly widely used because information technology is directly proportional to concentration, according to Beer'due south Law. Note that all of these measures are based on the RATIO of the ii intensities Io and I. This has the huge advantage of making these measures independent of the overall intensity of the light source and of the sensitivity of the detector used to mensurate the intensity. This in turn helps to make these quantities contained of the instrument used to measure out information technology.
8. Why does the Beer-Lambert Law lead to absorbances to a higher place 1?
An absorbance of ane only means that the transmitted intensity, I, is one-tenth of the incident intensity,
If y'all solve Beer's Law for concentration, you get:
c = A / (L* blastoff )
And then, you could determine the concentration c simply past measuring the absorbance A and dividing itby the product of the path length Fifty and absorptivity alpha. That is, if yous know alpha. Values of alpha are tabulated for many common molecules, but the trouble is that alpha varies every bit a function of wavelength, temperature, solvent, pH, and other chemic weather, so if the weather of your sample don't match those with which the blastoff was measured, the calculated concentration won't be accurate. Too, some spectrophotometers practice non follow Beer's Law exactly; it'due south not uncommon for some instruments to give absorbance readings that are a petty as well low and slightly non-linear with respect to concentration. Because of this, it's ameliorate to ready a series of southwardtandard solutions of known concentration, made up and so that the chemical atmospheric condition are as close every bit possible to those of the sample, measure their absorbances on your instrument, and plot a scale curve with concentration of the standards on the x-axis vs measured absorbance on the y-axis. Once the calibration curve is established, unknown solutions tin be measured and their absorbances converted into concentration using the calibration bend. Here is a graphic animation of this scale procedure practical to a specific analysis. This can be done either graphically (by drawing a line from the absorbance of each unknown across to the calibration curve and so down to the concentration axis) or it can exist washed mathematically (by plumbing equipment a line or bend to the calibration data, solving the equation of that line for concentration, then using that equation to convert measured absorbances to concentration). With computers, information technology's unremarkably easier to exercise the latter. The important point is that fifty-fifty if Beer's Law is not obeyed perfectly, you can still get authentic resulting using a calibration bend. 10
If you state Beer's Law every bit I = Io*10-(alpha*Fifty*c) , and so just divide both sides of the equation by Io , the result is I / Io = x-(alpha*50*c) = x-A, where A is absorbance. The quantity I / Io is defined as transmittance. Absorbance A is divers equally log( I / Io ). In principle, either transmittance or absorbance would work equally well for quantitative analysis, because there is exactly the same amount of data in an transmission reading every bit in an absorbance reading; 1 tin be converted to the other without loss. Yet, a calibration curve plotted in absorbance is linear, according to Beer's Police, whereas a calibration curve plotted in transmission would exist highly not-linear (exponential, in fact). It'south only easier to fit a line to a set of straight-line information, and to see when the data are deviating from that directly line, that to a fit a curved line to non-linear data, whether information technology is washed by hand or with a calculator or reckoner.
xi. What are the limitations of beer'south constabulary? What limits the linearity of Beer's Law plot?
Deviations from Beer'due south Constabulary tin exist caused by:
(a) Stray low-cal, which is whatsoever light striking the detector whose wavelength is exterior the spectral bandpass of the monochromator or which has not passed through the sample;
(b) Polychromatic light effect, which occurs if the absorber'due south absorption coefficient alpha varies over the wavelength interval of light passing through the sample;
(c) unequal light path lengths across the light beam;
(d) unequal absorber concentration across the light beam;
(e) changes in refractive index of the solution at high analyte concentration;
(f) light-scattering by the sample matrix, specially in turbid samples, resulting in a significant assimilation indicate even when the absorber'due south concentration is zero;
(g) shifts in chemical equilibrium involving the absorber every bit a part of concentration;
(h) changes in pH every bit a office of concentration.
(i) fluorescence of the absorber, in which some of the absorbed lite is re-emitted and strikes the detector;
(j) chemical reactions caused by the assimilation of light, including photolysis, dimerization, polymerization, and molecular phototropism (change in molecular shape when the molecule absorbs light).
(k) if the light intensity is extremely high (similar a focused laser), it's possible to observe not-linear optical effects, which are a central failure of the Beer-Lambert Law.
12. U 13. Why are measurements taken in increasing order of concentration when using spectrophotometry? fourteen. What happens to the free energy of the absorbed calorie-free exist 16. I see how the detector measures the transmitted intensity, I. How does it measure the incident intensit y, Io? 17. How do you use spectrophotometry to measure things that are colorless? xviii. Why does the Beer-Lambert Police crave monochromatic lite? 19. What is the low concentration limit of Beer's Law? 21. What is the musical instrument measurement range of manual in assimilation spectrophotometry? What is the optimum transmittance range for optimum precision? The measurement range of good-quality instruments is typically from an 22. Why are absorbance readings taken at the acme wavelength of maximum absorbance? Must you always use the maximum? What is the wavelength of least error? 23. How can you lot identify the cause of the deviation from Beer's Law ? 25. What is the minimum 28. How does Beer's Law employ to atomic absorption spectroscopy?
The virtually common of these are (a) and (b), which both event in a concave-downward curvature of the Beer's Law plot; (c) and (d) are easily avoided by proper experiment and musical instrument design (square cuvettes, well-mixed solutions); (east) is but a problem at very high concentrations; (f) is pretty mutual in existent-world applications to complicated samples, but can be minimized past special measurement techniques and instrument designs ; (chiliad) and (h) tin be avoided by buffering the solutions to constant pH and adjusting the concentration of reagents; (i) and (j) occur rarely with some particular absorber molecules and must be treated on a case-by-case footing; (yard) never occurs in standard laboratory instruments with conventional light sources..
The Beer-Lambert Law will non be obeyed if the photons of light striking the detector do not all have an equal chance of absorption by the sample. This tin happen if they have different absorption coefficients, different path lengths through the sample, or if they meet dissimilar concentrations of sample molecules. Likewise if anything else is nowadays in the sample that absorbs light or causes calorie-free handful, the measured absorbance will not be zero when the analyte's concentration is cypher, reverse to Beer'south Law. If the absorber undergoes any type of chemic reaction or equilibrium that varies equally a function of concentration, Beer'south Law will not be obeyed with respect to the overall or total concentration , because the concentration of the bodily arresting molecule is non proportional to the overall concentration of the solution. The "c" in Beer's Police refers to the concentration of simply the cushion, non to the total concentration of all the compounds reacting with or in equilibrium with the absorber. Even if Beer's Constabulary holds exactly for each individual chemical compound, the total absorbance of the mixture will not follow Beer'south Law with respect to the full concentration if the proportion of each chemical compound changes with concentration (unless by run a risk the absorptivity of all those compounds happens to be exactly the aforementioned).
By and large information technology'southward only a convention. Actually, the measurements tin be taken in whatever order; if the instrument and the samples and standards are stable with time, the upshot will be essentially the same.
Conservation of energy nonetheless works. The energy of the absorbed light is converted into heat, which increases the temperature of the measured samples slightly. But in an ordinary instrument the temperature increment is very minor and not even easily measurable. 15. How can the intensity of absorbed calorie-free exist measured ?
In absorption spectrophotometry the absorbed lite intensity is non measured direct, rather it's measured indirectly by measuring the difference between the incident and transmitted intensity.
If yous remove the sample from the light beam, the detector then measures the incident intensity,
Really the Beer-Lambert Police requires that all
There is no fundamental depression concentration limit, but at very low concentrations, the readings of absorbance tin be in error due to the limited resolution of the readout brandish or because of the betoken-to-dissonance ratio of the light intensity measurement (due to detector nose, photon noise, or light source fluctuation).
Normally, above whatever concentration produces an absorbance of nigh 2, deviations commencement to become apparent. Stray light especially becomes more than of import at loftier absorbances . Low-quality instruments, particularly when operated near their wavelength limits, exacerbate the non-linearity at high absorbances.
It really depends on what is the largest source of error. Taking the readings at the acme maximum is best at low absorbances because it gives the all-time indicate-to-racket ratio, which improves the precision of measurement.
There are ii experiments you tin can perform that volition throw at least some light on this question (pardon the pun). First, measure the absorbance of a single concentration at dissimilar path lengths (past using different sample cuvettes) and plot the measured absorbance vs path length (this is a Lambert's Law plot). Second, fix a series of standard solutions of different concentrations, measure then in a fixed path length, and plot concentration vs absorbance
Fit a straight line to the calibration data and look at a plot of the "residuals", the differences between the y values in the original information and the y values computed past the fit equation. Deviations from linearity will be much more than evident in the residuals plot than in the scale curve plot. (Click here for a backup-the-bare OpenOffice spreadsheet that does this for you lot . View screen shot). If the residuals are randomly scattered, then it means that the deviations are caused by random errors such as photon or detector noise or random volumetric or procedural errors. If the residuals accept a smoothen shape, this ways that the errors are systematic. If the residual plot has a directly line segment at low concentrations just curves off at high concentrations, then information technology'southward probably stray lite that is causing the non-linear region.
Information technology depends on the accuracy required. As a rough rule of pollex, if you need an accuracy of most 0.v%, you need an R 2 of 0.9998; if a 1% fault is good enough, an R ii of 0.997 will practice; and if a v% error is acceptable, an R 2 of 0.97 will exercise. The bottom line is that the R 2 must be pretty darned close to one.0 for quantitative results in analytical chemistry. But if the difference from linearity is shine and gradual, rather than random, you can even so get accurate results with a "curvilinear" calibration bend fitting technique, such as a quadratic or cubic fit. 26. What does information technology mean if the calibration curve (Beer's Law plot) does not extend through nothing?
If it'south close to nothing, it may merely exist due to random error in the absorbance readings or the volumetric preparations. Some other possibility is that the calibration curve shape is curved, but you have fitted a straight line to it; use a non-linear curve fit instead). Finally, it may mean that you lot have not properly subtracted the "blank" (see #16, above). 27. What is the consequence of the slit width on the spectra in uv-vis spectrophotometry?
The slit width determines the spectral bandpass, the wavelength range of the lite passing through the sample. The smaller the slit width, the more about monochromatic the calorie-free beam will be. Only if the slit width is too big, the polychromatic light effect will cause the spectral peaks to be shorter and broader than they would be at narrower slit widths. If yous are trying to measure out an authentic absorption spectrum, for example for apply as a reference spectrum for futurity measurements or for identification of that cushion, so you should employ a narrow slit. Notwithstanding, the signal-to-racket ratio decreases every bit the slit width is reduced, so information technology is not always practical to use the smallest slit width possible. If the spectral bandpass is one 10th (1/xth) of the spectral width (total width at one-half-maximum) of the narrowest ring in the spectrum, then the maximum peak top error acquired by polychromaticity will be less than 1%.
Beer'south Law is the basis of atomic absorption spectroscopy, as it is for conventional molecular spectrophotometry. Only there is a big difference. In atomic absorption, the absorbers are gratuitous atoms in the gas phase in a high-temperature flame or graphite furnace atomizer, and their absorption spectra consist of very narrow spectral "lines", only nearly 0.003 nm in width (compared to a typical molecule in solution that might have a spectral width of 50 - 100 nm or more). So in order for Beer's Law to be obeyed with such an extremely narrow assimilation, you would to utilize a light axle with an even narrower spectral width, ideally much less than 0.003 nm. Ordinary monochromators can not achieve a spectral bandpass anywhere nigh that narrow, so a conventional optical pattern is impossible. The problem is solved in two distinctly dissimilar means. The nearly common and least expensive type of
Fingerprints blot and besprinkle calorie-free slightly, fifty-fifty though they might not be readily visible. So a cuvette with fingerprints on it will give a slightly higher absorbance reading that a clean ane. Unless you compensate for this past by using the same cuvette, with the same verbal fingerprint, for the bare solution, and subtract the blank signal from the samples, the measured concentration volition be inaccurate. This is specially important if the absorbance is low (say, below 0.01 absorbance). 30. Why is absorbance non measured directly?
In absorption spectroscopy, the intensity of the captivated light tin not measured directly because the absorbed light is converted into heat, but the resulting temperature increment is far also small to be readily measured without very specialized and expensive equipment. The only thing that tin exist measured direct is the intensity of the transmitted beam. Making a calibration curve based on the intensity of the transmitted beam consequence not a good thought because the relationship to concentration is highly non-linear .
(c) 1991, 2015. This folio is part of Interactive Computer Models for Analytical Chemistry Instruction, created and maintained by Prof. Tom O'Haver , Professor Emeritus, The University of Maryland at College Park. Last updated August 2015. Comments, suggestions and questions should be directed to Prof. O'Haver at toh@umd.edu.
Number of unique visits since May 17, 2008:
Source: https://terpconnect.umd.edu/~toh/models/BeersLaw.html

0 Response to "what must you vary in order to obtain a beers law plot"
Post a Comment