Each Policy Should Contain Procedures and a Timetable for Periodic Review

This blog defines and compares the three most commonly used inventory command policies. It should be helpful both to those new to the field and also to experienced people contemplating a possible change in their company's policy. The blog also considers how need forecasting supports inventory management, choice of which policy to apply, and calculation of the inputs that drive these policies. Think of it as an abbreviated piece of Inventory 101.

Scenario

You are managing a detail item. The item is important enough to your customers that you desire to carry plenty inventory to avoid stocking out. However, the item is also expensive enough that you also want to minimize the amount of greenbacks tied up in inventory. The procedure of ordering replenishment stock is sufficiently expensive and cumbersome that you also desire to minimize the number of buy orders y'all must generate. Demand for the item is unpredictable.  So is the replenishment lead time between when you detect the need for more than and when it arrives on the shelf ready for use or shipment.

Your question is "How practise I manage this item? How practice I decide when to order more and how much to order?"  When making this decision there are dissimilar approaches you can use.  This blog outlines the most normally used inventory planning policies:  Periodic Order Upwards To (T, S), Reorder Point/Guild Quantity (R, Q), and Min/Max (s, Due south).  These approaches are often embedded in ERP systems and enable companies to generate automatic suggestions of what and when to order.  To brand the right decision, you'll demand to know how each of these approaches are designed to piece of work and the advantages and limitations of each approach.

Periodic review, order-upward-to policy

The shorthand notation for this policy is (T, S), where T is the stock-still fourth dimension between orders and S is the gild-up-to-level.

When to social club: Orders are placed like clockwork every T days. The used of a fixed reorder interval is helpful to firms that cannot continue runway of their inventory level in existent time or who prefer to event orders to suppliers at scheduled intervals.

How much to order: The inventory level is measured and the gap computed between that level and the gild-upward-to level S. If the inventory level is vii units and S = 10, then iii units are ordered.

Annotate: This is the simplest policy to implement but too the least agile in responding to fluctuations in need and/or lead fourth dimension. Also, note that, while the order size would be adequate to return the inventory level to Due south if replenishment were immediate, in practice at that place will be some replenishment delay during which time the inventory continues to drop, and then the inventory level volition rarely achieve all the way up Southward.

Continuous review, fixed order quantity policy (Reorder Point, Gild Quantity)

The shorthand note for this policy is (R, Q), where R is the reorder point and Q is the fixed club quantity.

When to order: Orders are placed as before long as the inventory drops to or below the reorder point, R. In theory, the inventory level is checked constantly, just in do information technology is normally checked periodically at the beginning or end of each workday.

How much to order: The society size is always fixed at Q units.

Annotate: (R, Q) is more responsive than (Southward, T) because information technology reacts more quickly to signs of imminent stockout. The value of the stock-still gild quantity Q may not be entirely up to you. Often suppliers can dictate terms that restrict your pick of Q to values compatible with minima and multiples. For example, a supplier may insist on an order minimum of 20 units and always exist a multiple of v. Thus orders sizes must be either xx, 25, 30, 35, etc. (This comment also practical to the two other inventory policies.)

Continuous review, order-up-to policy (Min/Max)

The shorthand notation for this policy is (s, South), sometimes called "little s, big S" where south is the reorder point and S is the order-upward-to level. This policy is more unremarkably called (Min, Max).

When to order: Orders are placed equally soon as the inventory drops to or below the Min. As with (R, Q), the inventory level is supposedly monitored constantly, but in practice information technology is usually checked at the cease of each workday.

How much to club: The club size varies. It equals the gap betwixt the Max and the electric current inventory at the moment that the Min is reached or breached.

Comment: (Min, Max) is fifty-fifty more responsive than (R, Q) because it adjusts the order size to take business relationship of how much the inventory has fallen below the Min. When demand is either zilch or ane units, a mutual variation sets Min = Max -one; this is called the "base stock policy."

Another policy choice: What happens if I stock out?

As you can imagine, each policy is likely to pb to a dissimilar temporal sequence of inventory levels (see Figure ane below). There is another factor that influences how events play out over time: the policy y'all select for dealing with stockouts. Broadly speaking, there are two main approaches.

Backorder policy: If you stock out, yous continue track of the lodge and fill up information technology after.  Under this policy, it is sensible to speak of negative inventory. The negative inventory represents the number of backorders that demand to be filled. Presumably, any client forced to wait gets commencement dibs when replenishment arrives. Y'all are likely to accept a backorder policy on items that are unique to your business that your client cannot purchase elsewhere.

Loss policy: If you stock out, the client turns to another source to fill up their order. When replenishment arrives, some new customer will go those new units. Inventory can never go beneath zero.  Cull this policy for commodity items that can hands be purchased from a competitor.  If you don't have it in stock, your customer will nigh certainly go elsewhere.

The role of demand forecasting in inventory command

Selection of control parameters, such as the values of Min and Max, requires inputs from some sort of demand forecasting process.

Traditionally, this has meant determining the probability distribution of the number of units that will be demanded over a fixed time interval, either the pb time in (R, Q) and (Min, Max) systems or T + lead time in (T, South) systems. This distribution has been assumed to be Normal (the famous "bell-shaped curve").  Traditional methods accept been expanded where the need distribution isn't assumed to be normal but some other distribution (i.e. Poisson, negative binomial, etc.)

These traditional methodologies have several deficiencies.

• Get-go, it usually ignores the problem of undershoot, in which demand drops inventory non simply to the reorder point but below it. Bold no undershoot leads to overestimates of service levels and fill rates.

• Second, the probability distribution of demand is very oftentimes non even close to "bell-shaped" or whatsoever causeless distribution was selected –  especially for items with intermittent demand such equally spares and service parts.

• Third, accurate estimates of inventory operating costs require analysis of the entire replenishment wheel (from one replenishment to the next), non merely the part of the cycle that begins with inventory hit the reorder point.

• Finally, replenishment lead times are typically unpredictable or random, not fixed. Many models presume a fixed pb fourth dimension based on an average, vendor quoted lead time, or average lead time + condom time.

Fortunately, better inventory planning and inventory optimization software exists based on generating a full range of random demand scenarios, together with random lead times. These scenarios "stress test" whatsoever proposed pair of inventory command parameters and assess their expected performance. Users can not only choose between policies (i.e. Min, Max vs. R, Q) but also determine which variation of the proposed policy is best (i.e. Min, Max of x,20 vs. 15, 25, etc.) Examples of these scenarios are given below.

The process of ordering replenishment stock is sufficiently expensive and cumbersome that you lot likewise desire to minimize the number of purchase orders you lot must generate

Choosing among inventory command policies

Which policy is right for you? There is a clear pecking order in terms of item availability, with (Min, Max) first, (R, Q) second, and (T, S) last. This order derives from the responsiveness of the policy to fluctuations in the randomness of need and replenishment. The social club reverses when because ease of implementation.

How do you lot "score" the operation of an inventory policy? There are two opposing forces that must be balanced: cost and service.

Inventory cost tin can be expressed either as inventory investment or inventory operating cost. The former is the dollar value of the items waiting effectually to be used. The latter is the sum of three components: property cost (the cost of the "care and feeding of stuff on the shelf"), ordering cost (basically the toll of cutting a purchase order and receiving that social club), and shortage cost (the penalization y'all pay when you either lose a auction or strength a customer to wait for what they want).

Service is ordinarily measured by service level and fill rate.  Service level is the probability that an item requested is shipped immediately from stock. Fill rate is the proportion of units demanded that are shipped immediately from stock. As a former professor, I call back of service level as an all-or-nothing grade: If a customer needs x units and you tin can provide only 9, that's an F. Fill rate is a partial credit grade: 9 out of 10 is ninety%.

When you lot decide on the values of inventory command policies, you are hitting a balance between price and service. Yous can provide perfect service by keeping an space inventory. You lot can hold costs to zero past keeping no inventory. You must observe a sensible identify to operate betwixt these ii ridiculous extremes. Generating and analyzing need scenarios can quantify the consequences of your choices.

A demonstration of the differences between two inventory command policies

We now show how on-hand inventory evolves differently under ii policies. The 2 policies are (R, Q) and (Min, Max) with backorders immune. To proceed the comparison fair, we set Min = R and Max = R+Q, use a stock-still pb time of five days, and subject both policies to the same sequence of daily demands over 365 simulated days of operation.

Figure i shows daily on-paw inventory under the two policies subjected to the same pattern of daily demand. In this example, the (Min, Max) policy has only two periods of negative inventory during the year, while the (R, Q) policy has 3. The (Min, Max) policy as well operates with a smaller boilerplate number of units on hand. Different demand sequences will produce different results, only in general the (Min, Max) policy performs better.

Note that the plots of on-manus inventory contain data needed to compute both price and availability metrics.

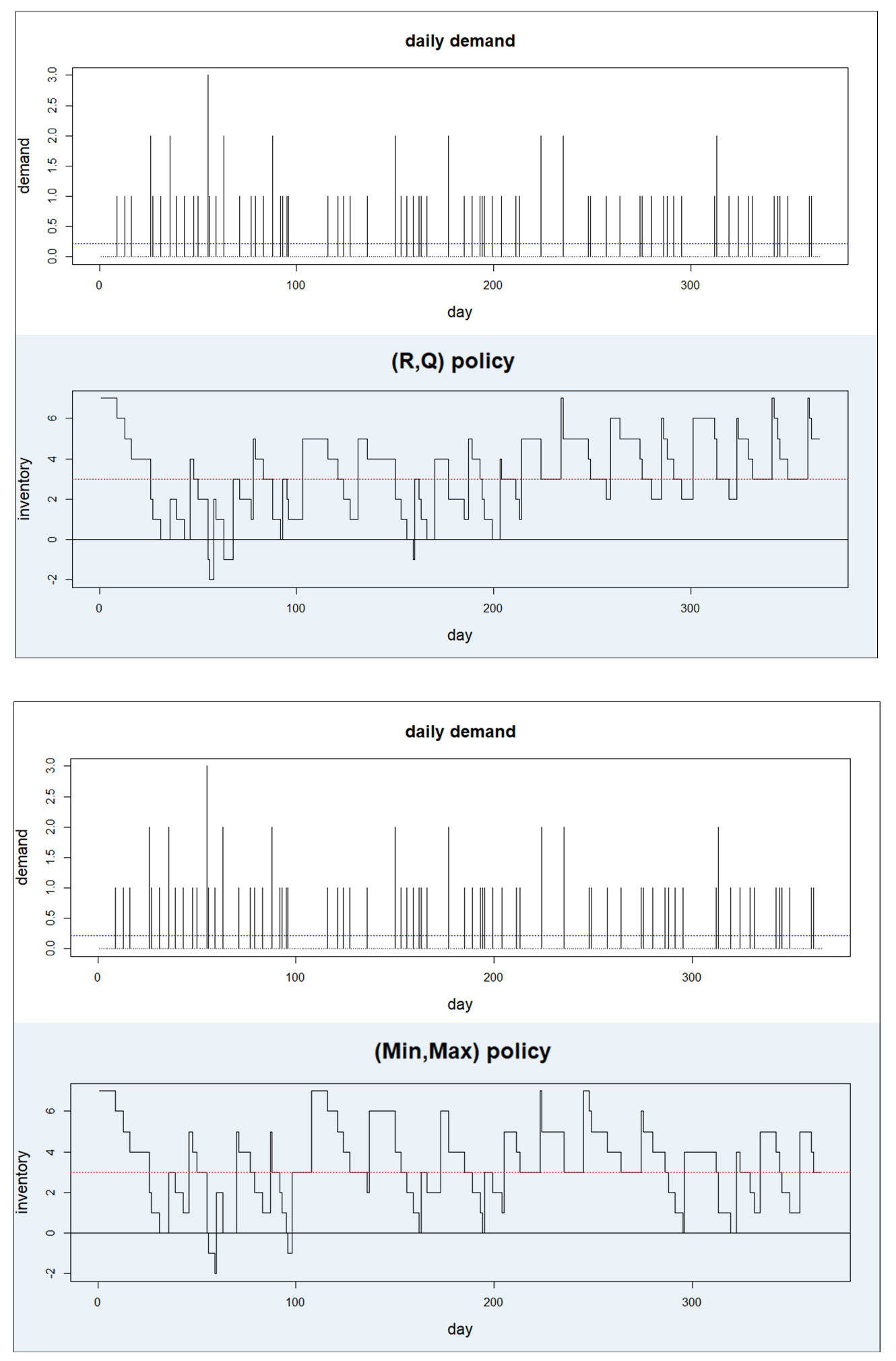
Figure one: Comparison of daily on-hand inventory under two inventory policies

Part of Inventory Planning Software

Best of Breed Inventory Planning, Forecasting, and Optimization systems can help yous make up one's mind which type of policy (is it better to apply Min/Max over R,Q) and what sets of inputs are optimal (i.east. what should I enter for Min and Max).  All-time of breed inventory planning and demand forecasting systems can assistance you develop these optimized inputs so that y'all tin can regularly populate and update your ERP systems with accurate replenishment drivers.

Summary

We defined and described the iii most commonly used inventory command policies: (T, S), (R, Q) and (Min, Max), along with the two most common responses to stockouts: backorders or lost orders. We noted that these policies require successively greater effort to implement just besides have successively better average performance. We highlighted the role of need forecasts in assessing inventory control policies. Finally, we illustrated how option of policy influences the twenty-four hours-to-solar day level of on-manus inventory.

Goldilocks Inventory Levels

You may think the story of Goldilocks from your long-ago youth. Sometimes the porridge was too hot, sometimes it was too cold, only but one time it was just right. Now that we are adults, we can interpret that fairy tale into a professional principle for inventory planning: At that place can be too little or too much inventory, and there is some Goldilocks level that is "merely right." This blog is nearly finding that sweet spot.

Phone call an Audible to Proactively Counter Supply Chain Racket

Y'all know the state of affairs: Y'all work out the best way to manage each inventory item past computing the proper reorder points and replenishment targets, and so average demand increases or decreases, or demand volatility changes, or suppliers' lead times alter, or your ain costs change.

An Instance of Simulation-Based Multiechelon Inventory Optimization

Managing the inventory across multiple facilities arrayed in multiple echelons can be a huge challenge for any company. The complexity arises from the interactions among the echelons, with demands at the lower levels bubbling up and any shortages at the higher levels cascading down.

stancilgated1948.blogspot.com

Source: https://smartcorp.com/inventory-control/inventory-control-policies-software/

Share this post